大津法由大津于1979年提出，对图像Image，记t为前景与背景的分割阈值，

前景点数占图像比例为 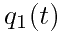，平均灰度为$$u_1(t)$$，方差为 $$D_1^2(t)$$；背景点数占图像 比例为$$q_2(t)$$，平均灰度为 $$u_2(t)$$，方差为 $$D_2^2(t)$$。图像的总平均灰度为：

$$u=q_1(t)*u_1(t) + q_2(t)*u_2(t)$$。

从最小灰度值到最大灰度值遍历t，当t使得值$$D_w^2=q_1(t)*D_1^2(t) + q_2(t)*D_2^2(t)$$

最小时 即为分割的最佳阈值 （ minimizes the weighte within class variance. ) 这个就意味着当取阀值为t时，前景和背景的方差加权和最小，即前景和背景每部分的像素都比较平稳。

 $$q_1(t)=\sum_{i=0}^{t-1}P(i)$$        $$q_2(t)=\sum_{i=t}^{255}P(i)$$                     ;                   $$u_1(t)=\sum_{i=0}^{t-1}\frac{i*P(i)}{q_1(t)}$$     $$u_2(t)=\sum_{i=t}^{255}\frac{i*P(i)}{q_2(t)}$$

$$D_1^2(t)=\sum_{i=0}^{t-1}[i-u_1(t)]^2\frac{P(i)}{q_1(t)}$$$$D_2^2(t)=\sum_{i=t}^{255}[i-u_2(t)]^2\frac{P(i)}{q_2(t)}$$;                            

$$D_1^2(t) q_1(t) = \sum_{i=1}^{t-1}[i-u_1(t)]^2P[i]=\sum_{i=0}^{t-1}i^2P[i]-2u_1(t)\sum_{i=0}^{t-1}i*P[i] + u_1^2(t)\sum_{i=0}^{k-1}P[i]$$

         $$ = \sum_{i=0}^{t-1}i^2P[i]-q_1(t)u_1^2(t)

同理可得        $$D_2^2(t)q_2(t) = \sum_{i=t}^{255}i^2P[i]-q_2(t)u_2^2(t)

                 $$D_2=\sum_{i=0}^{255}i^2P[i] - u^2 = D_w^2 + q_1(t)u_1^2(t) + q_2(t)u_2^2(t) - (q_1(t)u_1(t) + q_2(t)u_2(t))^2

                          $$=D_w^2+q_1(t)(1-q_1(t))u_1^2(t) + q_2(t)(1-q_2(t))u_2^2(t) - 2q_1(t)q_2(t)u_1(t)u_2(t)

                          =D_w^2 + q_1(t)q_2(t)(u_1^2(t) + 2u_1(t)u_2(t) + u_2^2(t))

                          =D_w^2 + q_1(t)(1-q_1(t))(u_1(t)-u_2(t))^2

$$Min(D_w^2)=Max(q_1(t)(1-q_1(t))(u_1(t)-u_2(t))^2)

Program

        q_1(t + 1) = q_1(t) + P[t + 1]

        u_1(t+1) = \frac{u_1(t)q_1(t) + P[t+1](t+1)}{q_1(t+1)}

        u_2(t+1) = \frac{u - u_1(t+1)q_1(t+1)}{1-q_1(t+1)}

 
<pre name = "code" class = "c++">
int MyImage::OtsuThreshMethod()
{
    double s0, s1, u0, u1, u2, maxv = 0, totsum = 0;
    int thr = 0, count = 0;
    if(!Histogram)
        GetHistogram();
    for(int i = 0; i < 256; i ++)
    {
        totsum += i *Histogram[i];
        count += Histogram[i];
    }
    s0 = 0; u0 = 0;

    for(i = 1; i <= 256; i ++)
    {
        s1 = s0 + Histogram[i-1];
        if(s1 == 0 )
            u1 = 0;
        else
            u1= (u0 * s0 + Histogram[i-1] * (i - 1))/s1;
        if(fabs(s1 - totsum) < 0.0001)
            u2 = 0;
        else
            u2 = (totsum - s1 * u1)/ (count - s1);
        if(s1 * (count - s1) * (u1 - u2) * (u1 - u2) > maxv)
        {
            maxv = s1 * (count - s1) * (u1 - u2) * (u1 - u2);
            thr = i;
        }
        s0 = s1;
        u0 = u1;
    }
    return thr;
}
</pre>